Moment of Inertia
Parallel Axis Theorem
What is the moment of inertia of ring about its diameter ?
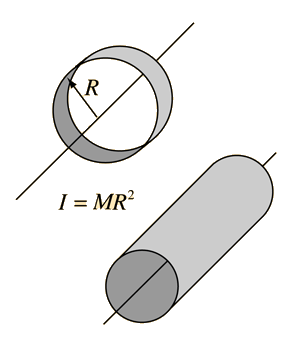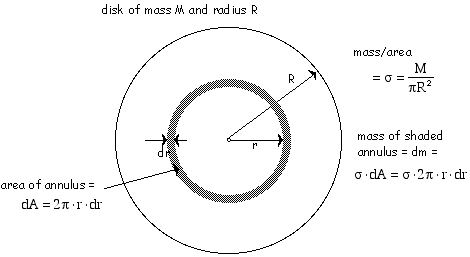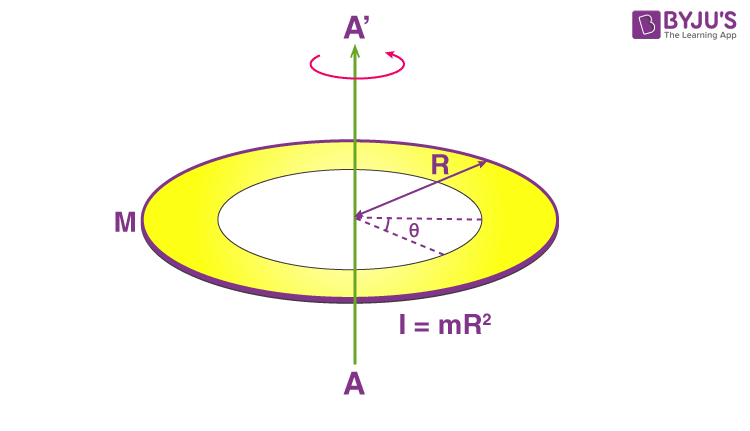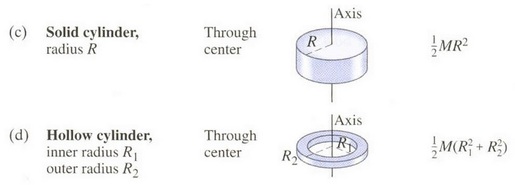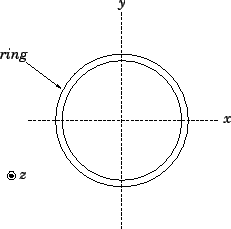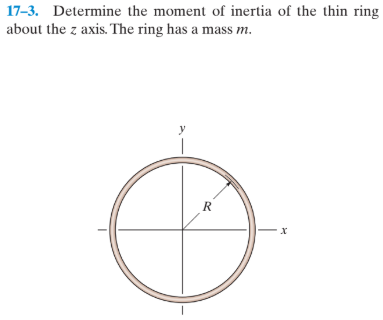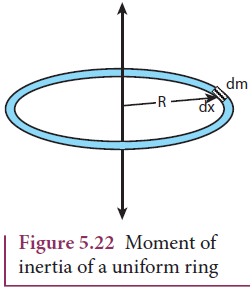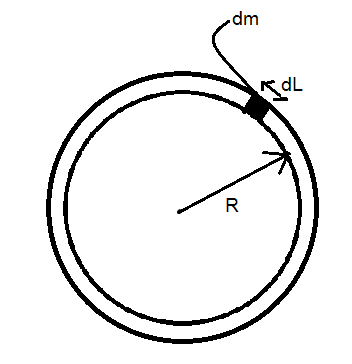
Calculate the moment of inertia of a thin ring of mass $m$ and radius $R$ about an axis passing through its center and perpendicular to the ring.
sep25_notes
Moment Of Inertia Of A Ring - Derivation and Calculation
The moment of inertia of ring about an axis passing through its diameter is `I`. Then moment of - YouTube
Mass Moment of Inertia
Formula: Thin circular ring (moment of inertia)
Moment of Inertia of Circular Ring about centre of mass and diameter #kamaldheeriya - YouTube
Deriving the moment of inertia for a hoop (ring) and disk - YouTube
Solved Determine the moment of inertia of the thin ring | Chegg.com
Solved The mass moment of inertia of a thin ring of mass m | Chegg.com
Answered: The mass moment of inertia of a thin… | bartleby
Determine the moment of inertia of a ring perpendicular to tangent and its plane. | Homework.Study.com
Moment of inertia of a ring of radius R whose mass per unit length varies with parametric angle θ according to the relation λ=λ°cos²θ, about its axis will be
Moment of Inertia Lab - Physics
The quarter ring shown has a mass m and was cut from thin, uniform plate. Knowing that r_1 = 34 r_2, determine the mass moment of inertia of the quarter ring with
Moment of inertia
How to calculate the moment of inertia of a thick circular ring about an axis passing through its centre perpendicular to its plane - Quora
Rotational Dynamics. Moment of Inertia The angular acceleration of a rotating rigid body is proportional to the net applied torque: is inversely proportional. - ppt download
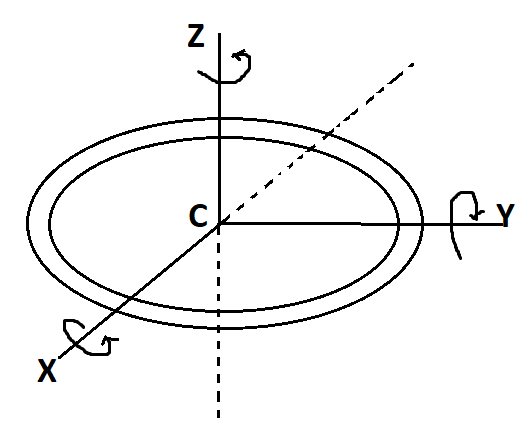
Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is $I$. What is the moment of inertia
Answered: 17-3. Determine the moment of inertia… | bartleby
Moment of Inertia, Thin Disc
Moment of Inertia of a Uniform Ring
